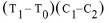La tabla siguiente muestra la posición de lectura, factores de medición teóricos y datos experimentales derivados de calibraciones por grupo para cada modelo de deformímetro. (Calibraciones individuales disponibles por un costo adicional; contacte a geokon para obtener más información.)
|
Modelo |
Posición de la lectura |
Factor de Calibre Teórico |
Factor de Lote Típico1 |
Factor de Calibre Típico1 |
Datos experimentales |
|
4200 |
D |
3.304 |
0.97 a 0.98 |
N/A |
3.237 |
|
4200 6 |
D |
N/A |
N/A |
N/A |
Ninguna |
|
4200 7 |
D |
N/A |
N/A |
N/A |
Ninguna |
|
4202 |
E |
0.391 |
0.91 |
N/A |
0.356 |
|
4204 |
A |
N/A |
N/A |
1.422 |
N/A |
|
4210 |
B |
N/A |
N/A |
0.3568 |
0.3423 |
|
4212 |
B |
N/A |
N/A |
0.3624 |
N/A |
|
4214 |
B |
N/A |
N/A |
0.3665 |
N/A |
1 El factor de medición exacto es determinado por la calibración real, no hay factor grupal que aplicar.
tabla 3: Factores de Deformímetro de Incrustación
7.1Posición A en la Consola de Lectura
Use la posición A para los modelos siguientes:
■Modelo 4204
■GK-404 (seleccione el modo de dígitos)
■GK-405 (convierta el período a dígitos usando esta fórmula:)
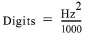
ecuación 1: Conversión de Período a Dígitos
7.2Posición B en la Consola de Lectura
Para lectura de mediciones en posición B, los factores de medición deben aplicarse al cambio en las lecturas. Estos factores de medición son factores de medición promedio para ese grupo de mediciones, o factores de medición para calibraciones individuales.
7.3Posiciones D y E en la Consola de Lectura
Lecturas para Modelos 4200 (posición D) y 4202 (posición E) se muestran directamente en microdeformaciones en la consola de lectura, con base en la ecuación teórica:
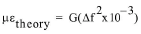
ecuación 2: Deformación Teórica
Donde:
f es la frecuencia en dígitos.
G es el factor de medición teórico, igual a 3.304 para el medidor 4200 y 0.3910 para el medidor 4202.
En la práctica, la acción de sujetar el cable acorta ligeramente la cuerda vibrante, provocando el sobre registro de la deformación. Esto puede ser compensado aplicando el factor grupal de medición proporcionado con cada medidor. Con el factor grupal de medición aplicado, el aparente cambio sobre la deformación mostrado en la consola de lectura es igual a:
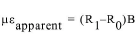
ecuación 3: Deformación Aparente
Donde:
R0 es la lectura inicial
R1 es la lectura actual de la consola de lectura, tomada en las posiciones D o E.
Nota: Cuando (R1 - R0) es positivo, la deformación es de tensión.
B es el factor grupal de medición proporcionado con cada medidor.
7.4Correcciones de Temperatura
Las variaciones de temperatura de magnitud considerable no son poco comunes, particularmente durante el proceso de curado del concreto; por lo tanto, siempre es aconsejable medir la temperatura al mismo tiempo que la deformación.
Expansión y contracción inducidos por la temperatura pueden aumentar los cambios reales en la tensión del concreto si el concreto está contenido de alguna forma. Estas tensiones se super imponen a cualquier otra tensión relacionada con la carga.
La temperatura también puede afectar al deformímetro. El aumento de la temperatura provocará que el cable vibrante se alargue, quedando flojo, indicando lo que podría interpretarse como una tensión de compresión en el concreto. Este efecto es equilibrado en cierto grado por un estiramiento correspondiente del cable, provocado por la expansión del concreto. Si la expansión en el concreto corresponde exactamente a la del cable, la tensión del cable permanecerá constante y no será necesaria ninguna corrección.
Sin embargo, el coeficiente de expansión del acero es diferente al coeficiente de expansión del concreto. Debido a esta diferencia, se requiere una corrección de temperatura igual a:
ecuación 4: Corregir los Efectos de la Temperatura Sobre el Medidor
Donde:
T0 es la temperatura inicial.
T1 es la temperatura actual.
C1 es el coeficiente de expansión del acero: 12.2 microdeformaciones/ºC.
(C1 para medidores Modelo 4200HT es de 17.3 microdeformaciones/ºC.)
C2 es el coeficiente de expansión del concreto: ~10 microdeformaciones/°C. (Los usuarios deben usar sus propios valores para C2 si los conocen.)
La deformación en el concreto relacionada con la carga (compuesta por la carga externa y los efectos de la temperatura) corregida para la temperatura, es determinada por:
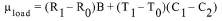
ecuación 5: Deformación Real, Relacionada con la Carga, Temperatura Corregida
Donde:
R0 es la lectura inicial.
R1 es la lectura actual de la consola de lectura, tomada en las posiciones D o E.
Nota: Cuando (R1 - R0) es positivo, la deformación es de tensión.
B es el factor grupal de medición proporcionado con cada medidor.
T0, T1, C1, y C2 son los mismos valores que se muestran en la Ecuación 4.
A continuación se muestra un ejemplo teórico de lo anterior.
Ejemplo:
Si:
R0 = 3000 en la posición D
R1 = 2900 en la posición D
T0 = 20 ºC
T1 = 30 ºC
B = 0.975 (factor de calibración grupal)
Entonces:
La deformación aparente = (2900 – 3000) 0.975 = –97.5 mdeformación (compresión).
La deformación relacionada con la carga, corregida para los efectos de la temperatura sobre el medidor = (2900 – 3000) 0.975 + (30 – 20) (12.2 – 10) = –75.5 microdeformaciones (compresión).
Nota: La deformación real que experimenta el concreto, (a saber, la que se mediría usando una escala de medición) se obtiene por la fórmula:
μactual = (R1 – R0) B + (T1 – T0) (C1)
Que en este ejemplo = (2900 – 3000) 0.975 + (30 – 20) (12.2) = 24.5 mdeformación (expansión).
Vea Apéndice G para más información.
7.4.1Correcciones para los Modelos 4200-6/4200-7
El efecto de la temperatura en los deformímetros 4200-6 y 4200-7 es complejo; varía dependiendo del nivel de presión. Un factor de corrección de temperatura típico para aplicarse al 10,000 με del modelo 4200-7 es el siguiente:
Factor de corrección de la temperatura = (0.000401*R1 - 1.067)(T1-T0)
Donde:
R1 es la lectura actual del medidor.
T1 es la temperatura actual en grados centígrados.
T0 es la temperatura inicial en grados centígrados.
Este factor de corrección fue desarrollado poniendo a prueba cuatro medidores en tres rangos diferentes (a saber, a los niveles de 4000, 8000 y 12000 microdeformaciones), a cinco diferentes niveles de temperatura (a saber, -40,
-20, 0, 20, 40 y 60 grados centígrados).
Cuando se utilice una expresión polinómica para calcular la deformación, el factor de corrección debe aplicarse a la lectura actual R1. Luego se agrega el valor modificado de R1 al polinomio.
Por lo tanto, el valor modificado de R1 que deberá agregarse al polinomio, es:
R1 + (0.000401*R1 – 1.067) x (T1 - T0)
Una propiedad conocida del concreto es su tendencia a encogerse cuando el agua que contiene disminuye, y a hincharse cuando absorbe agua. Este encogimiento e hinchamiento puede provocar grandes cambios en la deformación que no están relacionados a la carga ni a la tensión. La magnitud de estas deformaciones puede ser de varios cientos de microdeformaciones.
Es difícil compensar por estas deformaciones no deseadas. Puede intentarse manteniendo el concreto con un contenido constante de agua, lo que con frecuencia resulta imposible en estructuras de concreto expuestas a condiciones ambientales variables. El efecto de encogimiento e hinchamiento puede medirse colocando un deformímetro dentro de un bloque de concreto que no sea cargado, pero que esté expuesto a las mismas condiciones de humedad que los medidores activos. Las deformaciones registradas en este medidor pueden ser usadas como factores de corrección.
También es bien sabido que el concreto se deslizará bajo una carga sostenida. Lo que podría parecer un incremento gradual en la carga, demostrado por un incremento gradual en la presión, podría ser en realidad una tensión causada por el deslizamiento del concreto bajo una carga constante y sostenida.
En algunos proyectos, se han colocado medidores en bloques de concreto en el laboratorio que se han mantenido con carga mediante muelles en un bastidor de carga. De esta forma, puede cuantificarse el fenómeno del deslizamiento.
7.7Efecto del Crecimiento Autógeno
Algunos concretos más antiguos con una combinación particular de agregados y cementos alcalinos podrían expandirse con el paso del tiempo mientras experimentan cambios en su composición química y cristalización. Este proceso es conocido como crecimiento autógeno y es similar al deslizamiento, pero en la posición opuesta, y es difícil de cuantificar.
7.8Convertir Deformación a Carga
La carga es cualquier elemento estructural al cuál está fijado el deformímetro y se calcula usando la siguiente fórmula:
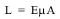
ecuación 7: Fórmula de Deformación a Carga
Donde:
L es la carga.
E es la constante de elasticidad del elemento estructural en las unidades adecuadas.
µ es la deformación en microdeformaciones.
A es el área de la sección transversal en las unidades adecuadas.
Al instalar deformímetros en pilotes de concreto, es una práctica estándar instalarlos por pares a cada lado del eje neutral. Esto permite corregir cualquier tensión impuesta por la inclinación tomando la deformación promedio de los dos medidores. También es una práctica estándar instalar un par de deformímetros cerca de la parte más alta del pilote. La medición de la tensión de estos dos medidores se utiliza para calcular el módulo del concreto.
Para las mediciones de tensión en algunos concretos durante las primeras etapas del proceso de curado, es importante conocer la constante efectiva del deformímetro. La constante efectiva de los diversos medidores de incrustación se muestra en la tabla siguiente:
|
Modelo |
E, aproximada |
|
4200 |
596,000 psi |
|
4200L |
56,500 psi |
|
4200-6 / 4200-7 |
N/A |
|
4200HT |
596,000 psi |
|
4200HT-T |
11,950,000 psi |
|
4202 |
610,000 psi |
|
4204 |
596,000 psi |
|
4210 / 4212 / 4214 |
2,350,000 psi |