Apéndice B.Teoría de la Operación

Una cuerda vibrante fija a la superficie de un cuerpo que está sufriendo una deformación se deformará en forma similar a la del cuerpo al que está fijo. Estas deformaciones alteran la tensión del cable, lo cual altera su frecuencia vibratoria natural (resonancia).

Los ejemplos a continuación se calcularon usando los parámetros para el medidor Modelo 4200. Sustituya los valores de la tabla de abajo para los Modelos 4202 y 4204.

Nota: Estas ecuaciones no aplican a los Modelos 4210, 4212, y 4214.

tabla 6: Parámetros Teóricos del Deformímetro de Incrustación

La relación entre la frecuencia (período) y la deformación (tensión) se describe a continuación:

1.La frecuencia fundamental (frecuencia resonante) de la vibración de un cable está relacionada con su tensión, longitud y masa. La frecuencia fundamental puede determinarse por la ecuación:

 

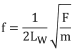
Donde:

L_w es el largo del cable en pulgadas.

F es la tensión del cable en libras.

m es la masa del cable por unidad de longitud (libras, segundos²/ pulgadas²).

2.Tenga en cuenta:

 

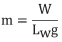
Donde:

W es el peso de L_w pulgadas de cable en libras.

g es la aceleración de la gravedad (386 pulgadas/segundos²).

3.Y:

 

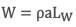
Donde:

ρ es la densidad del material del cable (0.283 libras/pulgada³).

a es la sección transversal del cable en pulgadas².

4.Combinando las ecuaciones de los pasos uno, dos y tres, se obtiene:

 

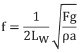
5.Note que la tensión (F) puede expresarse en términos de deformación, es decir:

 

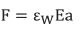
Donde:

Ɛ_w es la deformación del cable (pulgadas/pulgadas).

E es el módulo de Young del cable (30 x 10⁶ Psi).

6.Combinando las ecuaciones de los pasos cuatro y cinco, se obtiene:

 

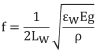
7.Sustituyendo los valores dados para E, g, y ρ se obtiene:

 

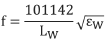
8.En la posición A, (que muestra el período de vibración, T) multiplicado por el factor de 10⁶:

 

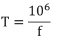
9.Combinando las ecuaciones de los pasos siete y ocho, se obtiene:

 

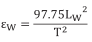
10.La ecuación del paso nueve debe ahora expresarse en términos de deformación en la superficie del cuerpo al que está fijo el deformímetro. Debido a que la deformación del cuerpo deberá ser equivalente a la deformación del cable:

 

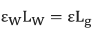
Donde:

Ɛ es la deformación en el cuerpo.

L_g es la longitud del medidor en pulgadas.

11.Combinando las ecuaciones de los pasos nueve y diez, se obtiene:

 

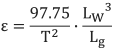
Donde: (para el Modelo 4200)

L_w es 5.875 pulgadas.

L_g es 6.000 pulgadas.

12.Por lo tanto:

 

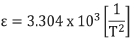
13.La visualización en la posición D de la consola de lectura se basa en la ecuación:

 

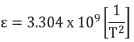
Elevar al cuadrado, invertir y multiplicar por el factor 3.304 x 10⁹ es realizado internamente por el microprocesador de la consola de lectura para que la lectura mostrada en la posición D está dada en micropulgadas por pulgada (ε).

Nota:    En los pasos anteriores, T se expresa en segundos x 10⁶ y ε se expresa en micropulgadas por pulgada.

Una alternativa es: ε = 3.304 x 10^-3 f² microdeformación.

En donde f es la frecuencia en Hz.